| |
Ermittlung der Zuverlässigkeit zerstörungsfreier Prüfungen mit der ROC-Methode |
| Die ROC-Methode (Receiver Operating Characteristics oder Relative Operating Characteristics) ist eine allgemeine Anwendung bei qualitativen Nachweisen, speziell in der zerstörungsfreien Prüfung und bei Human-Factors-Analysen. Sie ist immer dann zur Messung der Qualität bzw. der Zuverlässigkeit von Diagnoseverfahren anwendbar, wenn ein informationstragendes Nutzsignal von einem Empfängersystem (Receiver) aus einem Untergrund von Rauschen zu detektieren ist. Um welche Art von Signalen es sich dabei handelt – insbesondere ob es sich um qualitativ- oder quantitativ erfassbare Signalarten handelt – spielt keine Rolle. |
| Die Methode wurde zuerst in den vierziger Jahren zur Beurteilung von Radarsystemen herangezogen. Sie basiert auf der allgemeinen Theorie der Signaldetektion [1] innerhalb des Gebäudes des Systemtheorie und wird seit mehreren Jahrzehnten erfolgreich bei der Bewertung medizinischer Diagnosesysteme angewandt [2]. Im folgenden werden in kurzer Form die Grundlagen der Methode erläutert. Ausführlichere Darstellungen sind in [2 bis 4] zu finden. |
| In Bereichen der Zerstörungsfreien Prüfung (ZfP), als einem Spezialfall von Diagnoseverfahren, geht es in erster Instanz um die Entdeckung von Defekten in industriellen Bauteilen. Die Diagnosesignale können entweder quantitativ erfasst werden (z. B. die digitalisierte Ultraschallechohöhe) oder sind qualitativer Natur (z. B. das Schwärzungsbild auf einem Röntgenfilm). |
| Zur Charakterisierung der Qualität des Ergebnisses dienen zumeist die Defektauffindwahrscheinlichkeit (POD → Probability of Detection) und die Wahrscheinlichkeit für eine Falschindikation (PFI → Probability of False Indication), die in einem ROC-Diagramm aufgetragen werden. Bei automatischen elektronischen Systemen wird eine Statistik der Signale benutzt. Diese Charakteristika sind ein Maß für die Zuverlässigkeit desjenigen ZfP Systems oder Ensembles von ZfP Systemen, welches bei der Untersuchung zugrunde lag. Verallgemeinerungen für ähnliche Systeme sind jedoch möglich. |
| Weitere Methoden zur Charakterisierung der Qualität von ZfP-Verfahren sowie einen Einblick in die Probleme bei industriellen Anwendungen sind in den Proceedings der europäisch-amerikanischen Workshops zur Zuverlässigkeit zerstörungsfreier Prüfungen [5-6] zu finden. |
| In Blindversuchen mit industriell realistischen Einsatzbedingungen werden hierbei die prinzipiellen physikalisch technischen Fähigkeiten des Prüfverfahrens, die Faktoren der industriellen Einsatzbedingungen und der menschliche Faktor des ZfP-Systems integral geprüft. |
| Denkbar ist der Einsatz der ROC-Methode auch bei der Entwicklung von KI-Systemen. |
Erläuterungen zur ROC von ZfP-Systemen |
| Ein zerstörungsfreies Prüfsystem kann generell zu vier verschiedenen Diagnoseergebnissen kommen. |
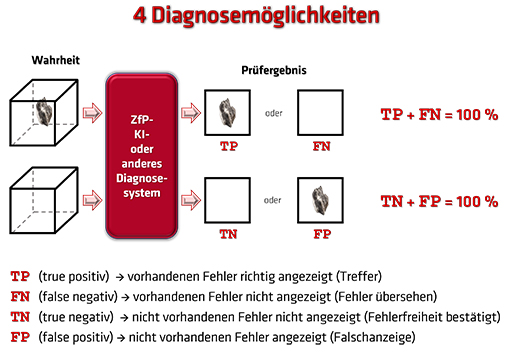
Abbildung 1 |
| Bemerkung: Die Bedeutung von positiv und negativ ist im medizinisch diagnostischen Sinne zu verstehen. |
| Ein gutes Prüfsystem wird sich also durch eine hohe Rate von TP (auf Kosten von FN) und eine geringe Rate von FP (zugunsten von TN) auszeichnen. Zur vollständigen Charakterisierung des ZfP-Systems reicht es aus, z. B. die Indikationen TP und FP aufzunehmen und deren relative Häufigkeiten in einem Diagramm darzustellen, da die Indikationen TP und FN zusammen 100 % der vorhandenen Defekte ergeben und die Fälle TN und FP sich zu 100 % der fehlerfreien Prüfabschnitte addieren. |
| Beachte: Die Detektionsrate und die Falschalarmrate (FAR) gehen für ausreichend große Zahlen an repräsentativen Testfehlern in die Wahrscheinlichkeiten für Richtig- und Falschanzeigen über, wenn die Population vollständig beschrieben ist. |
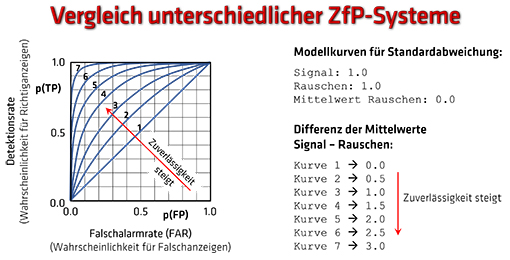
Abbildung 2 |
| Hierbei entspricht die Kurve 1 einer Zuverlässigkeit von 50 %, d.h. einer Zufallsgeraden. Das System 1 erzielt demnach stets mit gleicher Wahrscheinlichkeit richtige und falsche Prüfergebnisse, d. h. die Prüfung entspricht einer „Münze werfen“.Das System 7 dagegen (äußerste linke Kurve) entspricht einer sehr hohen Zuverlässigkeit und erzielt bei 96 %iger Wahrscheinlichkeit für richtige Aussagen nur 10 % an Falschaussagen. Bei einer Justierung auf 70 % Richtiganzeigen ist der Anteil der Falschanzeigen sogar kleiner als 2 %. Es ist zu erkennen, dass die Prüfqualität um so besser ist, je mehr sich die ROC-Kurve an die linke obere Ecke anschmiegt: Sie wächst von Kurve 2 bis 7 an und würde mit der Eckkurve durch den Punkt p(FP) = 0.0 und p(TP) = 1.0 ein ideales System repräsentieren, das bei 0 % Falschaussagen 100 % Richtigaussagen erzielt. Weiterhin kann aus dem Diagramm entnommen werden, dass die Größe der Fläche unter der ROC-Kurve ein gutes Maß für die globale Prüfqualität darstellt: Von der Kurve 1 bis zur Eckkurve wächst sie von 0.5 bis 1.0. |
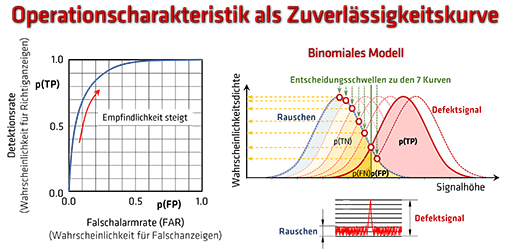
Abbildung 3 |
| Rechts im Bild ist das zugrunde liegende mathematische Modell skizziert. Für die Wahrscheinlichkeitsdichte des Auftretens eines Signals von den Defekten und dem Rauschen wird je eine Gaußverteilung als Funktion eines Defektparameters (z. B. Fehlergröße oder Signalamplitude) angenommen - was bei ausreichend großer Testkörperzahl fast immer zutrifft. Im Bild wird die Signalhöhe angegeben. Je eine ROC-Kurve ergibt sich für ein bestimmtes Signal-Rausch-Verhältnis. Der Abstand der beiden Gaußkurven von 2.5 gehört zu Kurve 6 (vergl. Abb. 2). Werden jetzt von großen Werten für den Schwellwert zwischen Signal und Rauschen zu kleineren (von rechts nach links auf der Ordinate) auf der Abszisse des binormalen Modells entlanggegangen und dabei jeweils die überstrichenen Flächeninhalte als p(TP) bzw. p(FP) Koordinaten eingetragen, so ergibt sich die ROC-Kurve von links unten nach rechts oben. |
| Charakteristik eines ZfP-Systems: Mit steigender Empfindlichkeit steigt die Wahrscheinlichkeit von Richtiganzeigen aber auch die Wahrscheinlichkeit der Falschanzeigen, da der Einfluss des Rauschens größer wird. |
Wie entsteht nun eine ROC-Kurve praktisch? |
| Zuerst müssen für eine Reihe diskreter Schwellwerte, welche angeben ob ein Signal einem Defekt- oder einem Rauschsignal zugeordnet werden soll, die TP und FP Indikationen gesammelt und relative Häufigkeiten berechnet werden. Das würde aber eine z. B. 5-malige Wiederholung der Prüfserien bedeuten. Beim Einsatz vollautomatischer Prüfsysteme ist dies kein Problem, bei Prüfauswertungen durch den Menschen behilft man sich an dieser Stelle mit der "rating confidence"-Methode. |
| Hierzu wird der Prüfer aufgefordert, seine Indikation über die Anwesenheit eines Fehlers mit einem Wahrscheinlichkeitsmaß zu versehen, z. B. - in einer diskreten Skala - ob der Fehler mit 100 %iger, 70 %iger, 50 %iger, 30 %iger Sicherheit anwesend oder mit Sicherheit kein Fehler da ist. Bei den bildgebenden Verfahren entspricht dies einer Skala der Fehlererkennbarkeit: sehr gut, gut, mittel, schlecht erkennbar oder kein Fehler da. |
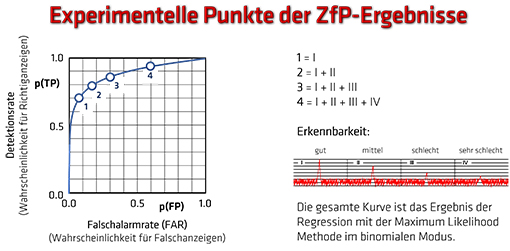
Abbildung 4 |
| Diese Angaben werden dann nach Richtig- und Falschaussagen sortiert und ergeben auf folgende Weise die 4 diskreten Punkte auf der ROC-Kurve: |
- die Indikationen mit der Erkennbarkeit "sehr gut";
- die Indikationen mit der Erkennbarkeit "sehr gut" und "gut";
- die Indikationen mit der Erkennbarkeit "sehr gut", "gut" und "mittel"
- die Indikationen mit der Erkennbarkeit "sehr gut", "gut", "mittel" und "schlecht".
|
| Schließlich wird mit dem 5. Punkt der rechte obere Eckpunkt erreicht, bei dem alle vorhandenen defekten bzw. leeren Prüfabschnitte aufsummiert sind. |
|
| Im Punkt 1 sind zumeist nur die größten (und daher nur ein Bruchteil der vorhandenen) Fehler enthalten und ein geringer Rauschanzeigen-Anteil, während im Punkt 4 fast alle (auch die kleinsten) Fehler enthalten sind, dafür aber auch ein beträchtlicher Rauschanzeigen-Anteil. Durch die so ermittelten experimentellen Punkte wird mittels eines „Maximum Likelihood“-Fits eine vollständige ROC-Kurve gelegt. |
Möglichkeiten von ROC-Untersuchungen |
| Bei der bisher beschriebenen ROC handelt es sich um die Detektions-ROC, da sie nur die Fehlerentdeckung beschreibt. |
| Zumeist wird die Frage nach der Zuverlässigkeit von ZfP-Systemen auf die Betrachtung der kritischen Fehler beschränkt. Mit „kritisch“ wird dabei die Zulässigkeit für die Funktionstüchtigkeit des Bauteils gemeint. Für diesen Zweck wird die maskierte ROC benutzt, bei der nur die "kritischen Defekte" bzw. die "nichtkritischen Prüfabschnitte" die statistische Basis bilden. |
| Wenn jedoch ein TP nur dann vergeben wird, wenn Detektion und Klassifikation des Fehlertyps richtig sind, entsteht eine verbundene ROC - an Stelle der Klassifikation kann hier auch die Richtignennung eines anderen Fehlerparameters abgefragt werden. Es ist ein wesentlicher Vorteil der vielseitigen ROC-Methode, dass jede Kombination von Parametern, ausgehend von dem gleichen Satz von Eingabedaten, untersucht werden kann. Die verbundene ROC erreicht die Oberlinie des Diagramms nicht, da sie zwar richtig detektiert, aber die falsch klassifizierten Indikationen fehlen. |
| Wir unterscheiden die verbundene ROC in 2 Stufen. |
- Bei der Joint-ROC muss der gefundene Fehler auch dem richtigen Fehlertyp zugeordnet sein.
- Bei der Combined-ROC muss der gefundene Fehler sowohl dem richtigen Fehlertyp als auch dem richtigen Schweregrad zugeordnet sein.
|
Anwendungsbeispiele |
| In der industriellen Prüfpraxis muss je nach der Sicherheitsrelevanz des beurteilten Bauteils – z. B. von einer simplen Wasserleitung, über ein Eisenbahnteil, eine Rohrleitung mit explosiven Chemikalien oder eine Schweißnaht an einem Kernreaktor – ein Kompromiß zwischen Kosten und Detektionserfolg geschlossen werden – d. h. den tatsächlichen Operationspunkt des Prüfsystems nahe der Punkte 1, 2, 3, bzw. 4 legen. Bei einer Wasserleitung ist das Sicherheitsrisiko begrenzt, jedoch die Kosten (Aufwand und Falschanzeigen) sind relevant, so dass Punkt 1 anzustreben wäre. Bei Defekten in einem Kernreaktor wird Punkt 4 gewählt, da das Auffinden aller relevanten Defekte wegen des Sicherheitsrisikos Vorrang hat. |
1. Zuverlässigkeit der Prüfer |
| Mehrere Prüfer werden unter gleichen Bedingungen zur Prüfung herangezogen. Die ermittelten Ergebnisse werden mit den wahren Daten verglichen. Jeder Prüfer erhält seine ROC-Kurve als Beurteilungskriterium seiner Zuverlässigkeit bei dieser Art der Prüfung. |
2. Zuverlässigkeit der Prüfverfahren |
| Es werden unterschiedliche Prüfverfahren jeweils von dafür qualifiziertem Personal untersucht. Die ermittelten Ergebnisse werden mit den wahren Daten verglichen. Es ist günstig, mehrere Prüfer einzusetzen und anschließend der Mittelwert zu bilden. So erhält jedes Prüfverfahren seine ROC-Kurve als Beurteilungskriterium seiner Zuverlässigkeit. Filmauswertung durch qualifizierte Prüfer Auswertung digitalisierter Bilder durch geschulte qualifizierte Prüfer automatische Auswertung Auswertung mittels Ultraschall Auswertung durch visuelle Betrachtung u.s.w. |
3. Zuverlässigkeit einer Prüfanweisung |
Es gibt z. B. mehrere Möglichkeiten, einen Fehler auf einem Röntgenfilm zu finden, durch:
- gezieltes Abdecken bestimmter Bereiche auf dem Film (helle Bereiche auf dem Film abdecken → bessere Erkennbarkeit durch das Auge möglich)
- unterschiedliches Festlegen der Auswerte-Intervalle
- Helligkeit des Leuchtkastens
- Benutzung einer Lupe erlaubt
Dies muss genau dokumentiert werden und bei der Auswertung beachtet werden. Die ermittelten Ergebnisse werden mit den wahren Daten verglichen. Jede Prüfanweisung erhält ihre ROC-Kurve als Beurteilungskriterium ihrer Zuverlässigkeit bei dieser Art der Prüfung. Das Festlegen von kleinen Intervallen zur Erhöhung der statistischen Basis ist sinnvoll, da ein Riss, der über mehrere Zentimeter verläuft, auch mehrmals richtig erkannt werden kann. |
Literatur |
Green, D.M. and Swets, J.A. „Signal Detection Theory and Psychophysics“, Wiley, New York (1966), reprinted by Krieger, New York (1974) p 47
Swets, J.A. and Pickett, R.M. „Evaluation of Diagnostic Systems“, Academic Press, New York (1982) ISBN 0-112-679080-9
Nockemann, C., Heidt, H., and Thomsen, N., „Reliability in NDT: ROC study of radiographic weld inspections“, NDT & E International 24(1991) pp 235-245
Swets, J. A., Signal Detection Theory and ROC-Analysis in Psychologie and Diagnostics, LEA Lawrence Erlbaum Associates, Publishers, Mahwah, New Jersey 1996
DGZfP, „European-American Workshop Determination of Reliability and Validation Methods on NDE“, Proceedings, Berlin, Germany, June 18-20, 1997, ISBN 3931381-18-8
ASNT, „American-European Workshop on Nondestructive Inspection Reliability“, Topical Conference Paper Summaries Book, September 21-24, 1999, Boulder, Colorado, USA, ISBN 1-57117-041-3
|
|
| Um die Zugangsdaten für den geschützten Bereich zu erhalten, laden Sie bitte das Formular (77 kB, pdf) herunter. Das ausgefüllte Formular ist über den dortigen Senden-Button per E-Mail zu senden. Wir werden uns dann mit Ihnen in Verbindung setzen. |
|
|